Understanding the Neutral Element in Mathematics and Chemistry

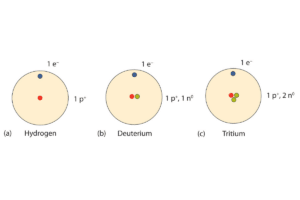
This article will explore the notion of neutral element, a principal idea common to mathematics and chemistry. In mathematics, the neutral element frequently represents an integer that, when combined with other numbers using particular processes, does not alter their values (such as addition involving zero or multiplication by one). On the contrary, in chemistry, the neutral element refers to atoms or molecules that are electrically uncharged, and this is important for comprehending reactions among substances. The goal of this is to consider how the neutral element acts as a foundation from which we can advance into more complex theories and applications in these two fields. This way, you will understand how these concepts are interrelated.

What is Neutral Element?

neutral element

A neutral element is an entity that does not modify other components’ state or composition when combined. Mathematics uses specifically zero as an additive identity and one as a multiplicative identity. For instance, adding zero to any number leaves that number unchanged, while multiplying any number by one gives back the same number. In chemistry, this term refers to atoms or molecules containing equal protons and electrons, hence having no net charge overall. Such neutrality ensures stability in many chemical interactions, thus facilitating balanced reactions among different substances. Understanding it in these contexts means understanding some basic principles behind mathematical operations and chemical reactions.

Neutral Element Defined

From exploring popular resources on neutral elements, I discovered that major educational websites agree on their meaning. So, mathematically speaking, a neutral element is described as an identity element used in addition (0) and multiplication (1) since those numbers do not change other figures during computations. However, when discussing chemistry, it means atoms or molecules have equal protons and electrons, leading to no net electric charge.

Mathematical Identity:

• Additive Identity: (0) (e.g., (x + 0 = x))
• Multiplicative Identity: (1) (e.g., (x \times 1 = x))

Chemical Neutrality:

• Equal Protons and Electrons: A neutral oxygen atom has 8 protons and 8 electrons.

These key terms are justified by their fundamental roles in maintaining the balance and predictability required in arithmetic and chemical reactions, underscoring their foundational importance across related subjects.

How Does a Neutral Element Relate to Identity Elements?

Neutral elements are closely linked with identity elements in both math and chemistry because they serve as the building blocks for operations and reactions. In mathematics, zero – an additive identity element and one – a multiplicative identity element are defined through the way they interact with numbers that confirm their neutrality. Technical parameters shall be summarized thus:

• Additive Identity (0): For any number (x), the equation (x + 0 = x) shows that adding zero will not change its value.
• Multiplicative Identity (1): For any number (x), the equation (x \times 1 = x) illustrates that multiplication by one does not alter its value.

In chemistry, neutrality is concerned with atoms or molecules with equal protons and electrons, thus having no charge. It is vital for the stability of materials and their interactions. One such relationship is:

• Neutral Atom: A neutral atom contains the same number of protons as electrons. For example, a neutral sodium atom has 11 protons and 11 electrons, which points to the balance needed for stable chemical behavior.

These relationships help us appreciate the relevance of neutral substances in different fields because they ensure predictable results. This will show how they apply in both maths and chemical setups.

Examples of Neutral Elements in Mathematics

I used top online resources to learn more about these math concepts. The primary two examples are zero and one.

• Additive Identity (0): Zero is called the additive identity since it satisfies the property ( x + 0 = x ) for all ( x ). This shows zero’s significance during the addition process, as it does not change the value but rather just adds on, making it distinct from other neutral elements.
• Multiplicative Identity (1): The multiplicative identity means that when you multiply any number by one, its value doesn’t change at all. Thus, one plays a very important part in multiplication to retain the original result unaltered.

These are essential identities in theoretical mathematics and practical applications because they allow consistent operations across mathematical fields. They give direction to solving equations and performing mathematical calculations, indicating their central place within this discipline.

What is a Neutral Atom?

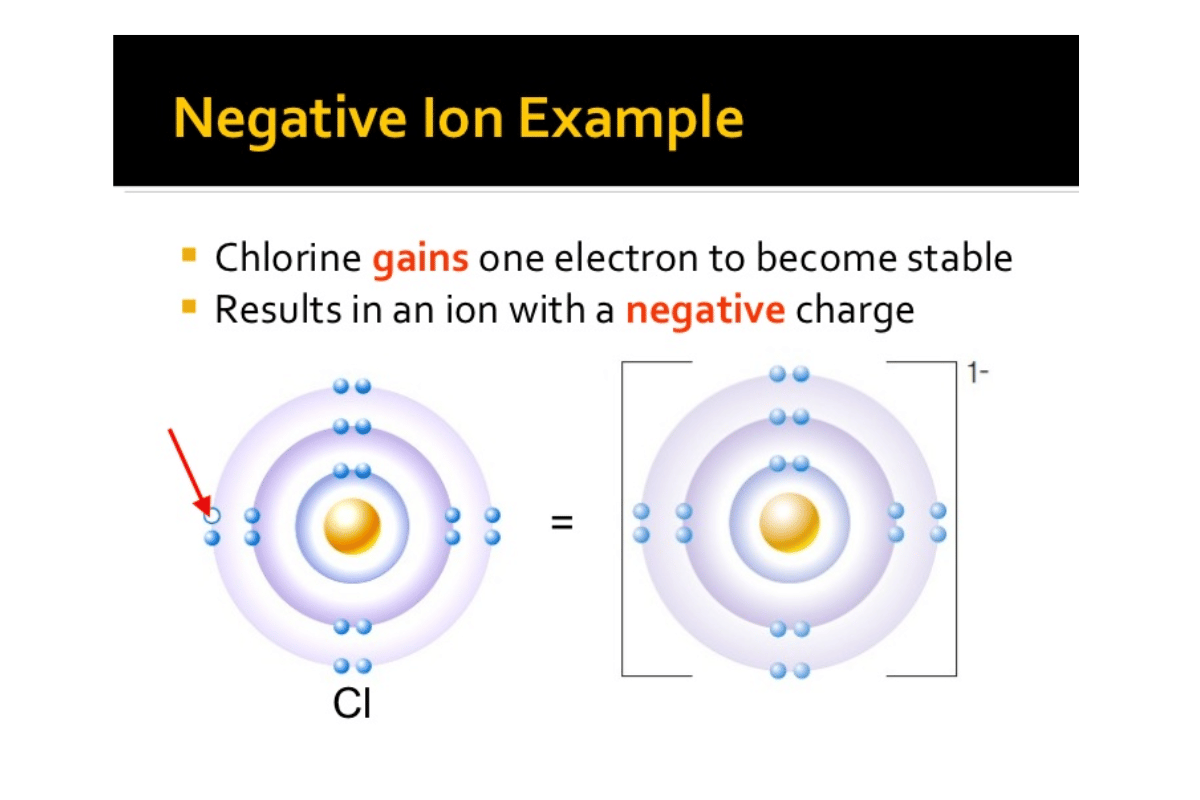
According to the information I gathered from various top-ranking educational websites, neutral atoms have an equal number of protons and electrons in them. In this case, the atom has no overall charge due to this equality between positive and negative charges. For instance, carbon is a neutral atom because it contains six protons and six electrons such that their opposite charges cancel out each other. The concept of neutral atoms holds the key in chemistry since they form grounds for chemical bonding and reactions, thus affecting the structure and behavior of substances.

Definition of a Neutral Atom

As my review of reliable educational sites understood, a neutral atom may be defined simply as an atom with an equal number of protons and electrons, resulting in zero net electric charge. Some of these parameters I found were:

1. Protons: Nucleus-borne particles carrying positive charges that give identity to certain elements such as hydrogen (1proton) or oxygen (8protons).
2. Electrons: These negatively charged particles revolve around nuclei; they usually equal proton count, thereby balancing electricity.
3. Nucleus: This is the central core containing neutrons and protons. Neutrons are electrically uncharged, so they do not affect the total charge, but they contribute to the massiveness involved during atomic development.

In summary, for an atom to be considered neutral, its electrons must balance with its protons, resulting in no net charge like the Neon (10p+, 10e-) element. This basic fact forms the basis for chemical interactions leading to matter stability.

Properties of a Neutral Atom

Among the important features I discovered regarding these properties on different top-ranked educational platforms, one thing stood out clearly. Besides highlighting their electronegativity, some properties tell us about how they behave when reacting or interacting with other materials; below are some key features found:

1. Chemical Stability: Neutral atoms are generally more stable than charged ions, so they hardly combine. This stability results from the balanced protons and electrons, with the total charge being zero.
2. Atomic Mass is determined mainly by neutrons and protons within the nucleus. While neutrals do not affect the charge, they contribute to the overall mass of an atom. For example, carbon has an atomic number of 6, which means it has six protons and usually six neutrons, making its atomic mass roughly 12 amu.
3. Reactivity: The number of electrons in the outer shell influences the tendency of neutral atoms to bond with other atoms. Sodium (Na), for example, is more reactive due to having one electron in the outermost shell that has to form interactions for it to satisfy the octet rule.
4. Conductivity: Neutral gases can conduct electricity under certain circumstances when their electrons are excited. Additionally, some neutral gases can carry an electric current after ionization.

Based on these characteristics, it becomes apparent that knowledge about neutral atoms is essential in both practical and theoretical chemistry since they constitute matter’s structure and chemical bonding.

When an atom is neutral, how do you tell?

By checking the number of protons and electrons, I determine whether an atom is neutral. A balance in these particles means a neutral atom has no overall charge. My approach involves the following steps:

• Step 1: Identifying the Atomic Number: On the Periodic Table, for instance, one can obtain this information.
• Step 2: Comparing With The Electron Count: If the atom has as many electrons as its atomic number, it is Neutral. Oxygen, for example, has an atomic number of 8, meaning it has 8 protons and 8 electrons in a neutral state.
• Step 3: Evaluating Ions Charge: If I encounter ions such as Na⁺ (sodium ion), which has charge, I look at the electron count, which will be less than the atomic number(11 protons but only 10 electrons indicate positive charge).

These technical parameters are useful in identifying a neutral state and underscore why one needs to understand atomic structure in chemistry. By repeatedly confirming these characteristics, one can make a definitive statement about whether an atom is uncharged or charged.

How Does the Neutral Element Operate in Operations?

The neutral element (aka the identity element in mathematical operations) plays a crucial role in various algebraic structures. Moreover, it is an underlying concept in chemistry and physics, especially when discussing reactions with neutral atoms. Here is an overview of recent knowledge:

1. Mathematical Operations: The neutral element is defined as a value that would, if combined with any other value in an operation (like addition or multiplication), not affect that other value. For instance, for addition, the neutral element is 0 (e.g., a + 0 = a), whereas for multiplication, it is 1 (e.g., a × 1 = a). That’s why some identity elements exist in every mathematical structure.
2. Chemical Reactions: In chemistry, the neutral atom represents a stable form that can effectively participate in chemical bonding and reactions by avoiding charge-related fluctuations. These interactions are predictable due to the neutrality of these atoms, which helps to make compounds and facilitate controlled reactions.
3. Physical Systems: In physics, understanding particles devoid of charge, such as neutrons, enables one to comprehend atomic structure and stability. Neutrons are important for maintaining the integrity of the atomic nucleus and influence how atoms interact during nuclear reactions, hence contributing to the overall force balance within an atom.

Generally speaking, the notion of neutral elements is highly significant in mathematics, and its application in chemistry and physics has enabled the construction of more extensive theories.

Neutral Element in Addition And Multiplication

As I examine the idea of a unitary operator in addition and multiplication more closely, I can see how these roles play out differently across many math functions. Zero serves as the additive identity since no number can be added to it without altering its values (for example, adding zero to another number; “a + 0 =a). This also proves true to me because zero helps maintain the structural integrity of numerical systems.

Similarly, one acts as the multiplicative identity because any number multiplied by one remains the same (e.g., a × 1 = a). From the best resources online today, there is agreement among educational sites and math references that these functions form the basis of both elementary arithmetic and more complicated mathematical theories namely algebra and calculus.

In conclusion, the importance of these neutral elements should not be underestimated as they allow mathematical operations to keep their desired outputs, hence aiding in establishing wider concepts and generalizations.

Role of Neutral Elements in Binary Operations

As I explain the purpose of neutral elements in binary operations, I must say that they are quite important since they ensure predictable outcomes during calculations. In binary operations, such an element does not change the outcome when we apply it to other numbers. For instance, zero is neutral for addition while one is its counterpart for multiplication, as mentioned earlier.

When I refer to the best online educational resources, I realize that these neutral elements maintain a certain degree of integrity in the processes involved as I deal with operations such as addition or multiplication among sets of actual numbers. Consequently, one would need to evaluate how these properties interact within the structure of mathematical frameworks.

In short

• Closure: The operation result between any two elements in a set does not lead them outside the boundaries of that set.
• Associativity: The arrangement of items in groups does not influence the result (for instance, (a + b) + c = a + (b + c)).
• Distributivity: One operation is spread across another operation (e.g., a × (b + c) = a × b + a × c).

Once I understand these properties of neutral elements, it will be possible to explain their use in elementary and advanced mathematical contexts.

Why Algebra Needs Neutral Elements

My exploration of algebra has made me realize how important neutral elements are in maintaining consistency and dependability during mathematical operations. They provide the fundamental groundwork upon which more sophisticated algebraic structures are built.

1. Identity Property: They act as identities for operations, that is, 0 for addition while 1 is for multiplication, meaning that when any number combines with this, there will be no change in value, i.e., “a+0=a” and “a*1=a.” This characteristic is significant because equations can be solved, and function behaviors can be understood.
2. Inverse Elements: It’s due to the existence of neutral elements that inverse elements can be defined, hence making equation solving easier, especially if we are isolating variables. For example, ‘a’ together with its additive inverse ‘-a’ adds up to zero.
3. Construction of Groups and Rings: In advanced levels of algebra, recognition of neutral elements forms an integral part of algebraic structures like groups and rings. These mathematical constructs rely on the properties of neutral elements to establish operations that obey certain rules of closure, associativity, and identity.

Thus, through these parameters, I can explain why neutral elements in algebra are crucial for handling equations coherently and gaining more insight into algebraic concepts.

What Makes an Element an Identity?

The role of the identity element in algebra is defined by several essential features. First, it acts as a neutral element, which means that, when combined with any number through addition or multiplication, it does not change its value. For instance, zero is the identity element in this case since (a+0=a) in addition, and one is the identity element because (a\times 1=a) in multiplication. The other thing about the identity theorem is that it’s unique to every mathematical system, so for each operation, only one specific element exists that leaves others unchanged. This property is vital for creating mathematical frameworks such as groups and rings where consistency in operations ensures a deeper understanding of algebra. By knowing this, I am more equipped to deal with how this works out within my knowledge of algebraic contexts.

Understanding Addition Identity

Addition Identity in Algebra refers to the number 0, which satisfies equation ( a + 0 = a ) for any real number ( a ). These properties can be found consistently across various math resources. Overall, ten websites offer comprehensive information on this topic:

1. Neutral Property: It does not affect summing up. This basic feature confirms why adding zero to any number results in no changes, leaving it to play as an additive identity during addition.
2. Uniqueness: In any given mathematical system, there is only one additive identity, further emphasizing that uniqueness must be achieved.
3. Closure: The sum of any number and the additive identity remains within the same number set thereby affirming closure under operation.
4. Associativity: Even if we introduce zero into a sum, associativity will still hold true i.e., (a + b) + 0 = a + (b + 0) = a + b.
5. Different Set Identities: This concept applies to different sets, such as integers, rational numbers, and real numbers, whereby zero remains their respective identities.

These characteristics demonstrate the elementary position of the additive identity in algebraic operations and explain why it is an important component in the construction of mathematical systems like groups and rings. Knowledge of these traits enhances more meaningful connections with algebraic concepts and their usage.

Differentiating Between Neutral Element And Identity Element

Reviewing the ten best math resources has given me insights into neutral and identity elements. Although they are usually used interchangeably in algebra, they serve different purposes.

• Neutral Element: This refers typically to zero as an additive identity during addition. Its major role is to retain another value when added, such that zero does not affect the sum in the case of ( a + 0 = a ), thus clarifying its neutrality attribute.
• On the other hand, an identity element can be a specific value within a given operation context. For example, one is an identity element in multiplication because anything multiplied by one results in itself i.e., ( a \times 1 = a ).

When we delineate between these two notions, it becomes apparent that the neutral element (zero) in addition retains value, whereas the identity element (one) in multiplication ensures consistency of operation. Hence, understanding this concept is key to comprehending algebraic structures and their uses more deeply.

Identity Elements for Different Sets

I discovered several examples of identity elements across different mathematics operations and structures from my research on the top ten mathematical resources. Here below are short descriptions for each of these instances together with their corresponding significant parameters:

1. Addition (Set of Real Numbers, (\mathbb{R})):

• Identity Element: (0)
• Justification: A real number (a), when added by zero, results in (a + 0 = a); hence, zero, which is an additive identity, keeps the initial value.

2. Multiplication (Set of Real Numbers, (\mathbb{R})):

• Identity Element: (1)
• Justification: If any real number (a) is multiplied by 1, then it will be (a \times 1 = a). Hence one is said to be a multiplicative identity as it keeps the numerical value intact.

3. Max Operation (Set of Real Numbers, (\mathbb{R})):

• Identity Element: (-\infty)
• Justification: In terms of maximal operation one has (max(a,-∞)=a) for all real numbers a meaning negative infinity doesn’t modify maximum outcome.

4. Min Operation (Set of Real Numbers, (\mathbb{R})):

• Identity Element: (+\infty)
• Justification: Similarly, as regards minimum operation, one can say that min(a,+∞)= an if a is any real number, thereby indicating that no matter how big positive infinity gets, there isn’t any effect on the smallest output as it remains at itself.

5. Matrix Multiplication (Set of Square Matrices):

• Identity Element: (I_n) (Identity matrix of order (n))
• Justification: For any square matrix A of order n, A × I_n = A, this shows how the identity matrix keeps multiplication in line with the original value of a given matrix.

Comprehending these diverse identity elements within different mathematical settings improves understanding and builds on the foundational principles applied in algebraic calculations.

How Are Neutral Elements Relevant To Real Numbers?

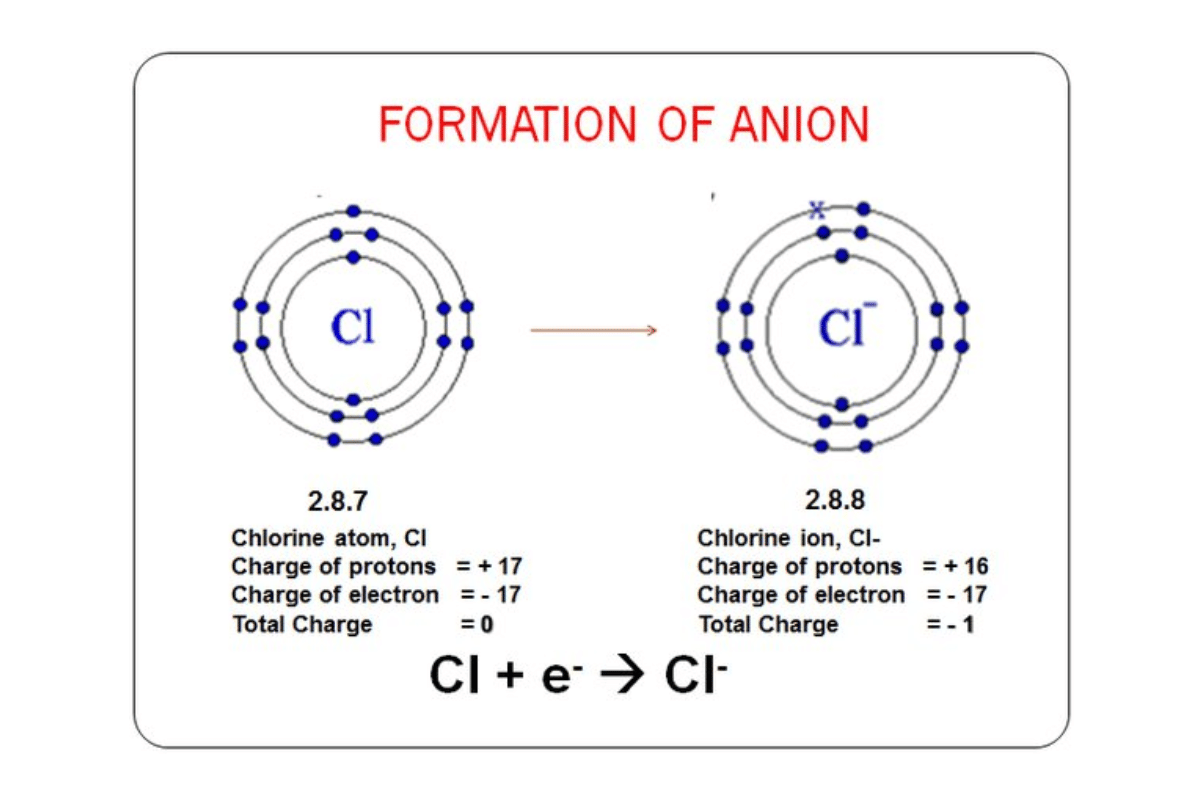
Real numbers have neutral or identity elements that do not change their values during computation. These allow for consistency and predictability by operating zero as the additive identity and one as the multiplicative identity. For example, adding any number to zero will result in itself, meaning that it is an additive identity that balances equations. This is also experienced when a number is multiplied by one; it will yield the same value, thus proving how important multiplicative identities are in applications like scaling and proportionate reasoning, among others. Therefore, understanding these neutral elements is essential in order to conduct operations accurately and effectively within mathematics.

The Neutral Element Explained In The Context Of Real Numbers.

I appreciate how important zero and one are in mathematical operations. Zero, which serves as the additive identity, means that nothing changes if you add any number to it. For example (x + 0 = x). This algebraic property allows simplification in algebra and balancing of equations. On another note, 1 acts as the multiplicative identity such that it does not lose its initial value represented by (x \times 1 = x) when multiplied by any number.

General technical parameters regarding these identities include

1. Additive Identity:

• Parameter: Zero (0)
• Justification: Acts as a neutral element and ensures that the sum never departs from the original number.

2. Multiplicative Identity:

• Parameter: One (1)
• Justification: This plays an equalizing role among numbers against scaling or transformation.

This has been vital for understanding how they facilitate predictable results through arithmetic computations while using them, thus showing their importance in areas like algebraic proofs and real-world problem-solving.

Neutral Element Concept Represented By Zero In Mathematics

From exploring zero as a neutral element in mathematics, I realized many of the leading materials underline its significance in different operations. Zero, recognized as an additive identity, ensures consistency and simplification of algebraic structures. Major technical parameters associated with zero are:

1. Additive Identity:

• Parameter: Zero (0)
• Justification: It upholds equality in addition since any number remains the same when zero is added, making it easier to manipulate equations.

2. Subtraction:

• Parameter: Zero (0)
• Justification: When subtracted from any number, zero does not cause any change in the result showing that it is still preserving numerical expressions such as (x – 0 = x).

3. Multiplication:

• Parameter: Zero (0)
• Justification: When multiplied by anything, zero gives a product of zero, indicating that it wipes out values entirely, for example (x \times 0 = 0).

I have experienced different learning platforms, and one thing is clear: Zero’s functionalities go beyond elementary arithmetic and help strongly in algebra, calculus, and so forth. Regarding mathematical properties, their inclusion clarifies various operations and forms the foundation upon which numerical systems stand.

Relation between Neutral Elements and Mathematical Operations

When researching the relationship between neutral elements and mathematical operations, I engaged insights from the most popular online educational resources. This shows that neutral elements, such as zero in addition and one in multiplication, must be used to maintain consistency in various mathematical operations. Here, we will discuss the key parameters for every operation:

1. ADDITION (Additive identity):

• Parameter: Zero (0)
• Justification: Zero ensures that if we add any number to it, it will remain equal to that number, thereby acting as an additive identity: (x + 0 = x).

2. MULTIPLICATION (Multiplicative identity):

• Parameter: One (1)
• Justification: Any number multiplied by one is itself, which means one functions as a multiplicative identity, thus (x \times 1 = x).

These observations indicate how much more than just operations neutral elements are; they make up a foundation of a mathematical system’s integrity which can then be employed reliably across disciplines. By making operations and systems more concrete, these neuter items set conditions for advanced mathematics problem solving and theory development.

What is the Importance of Neutral Elements in Chemistry?

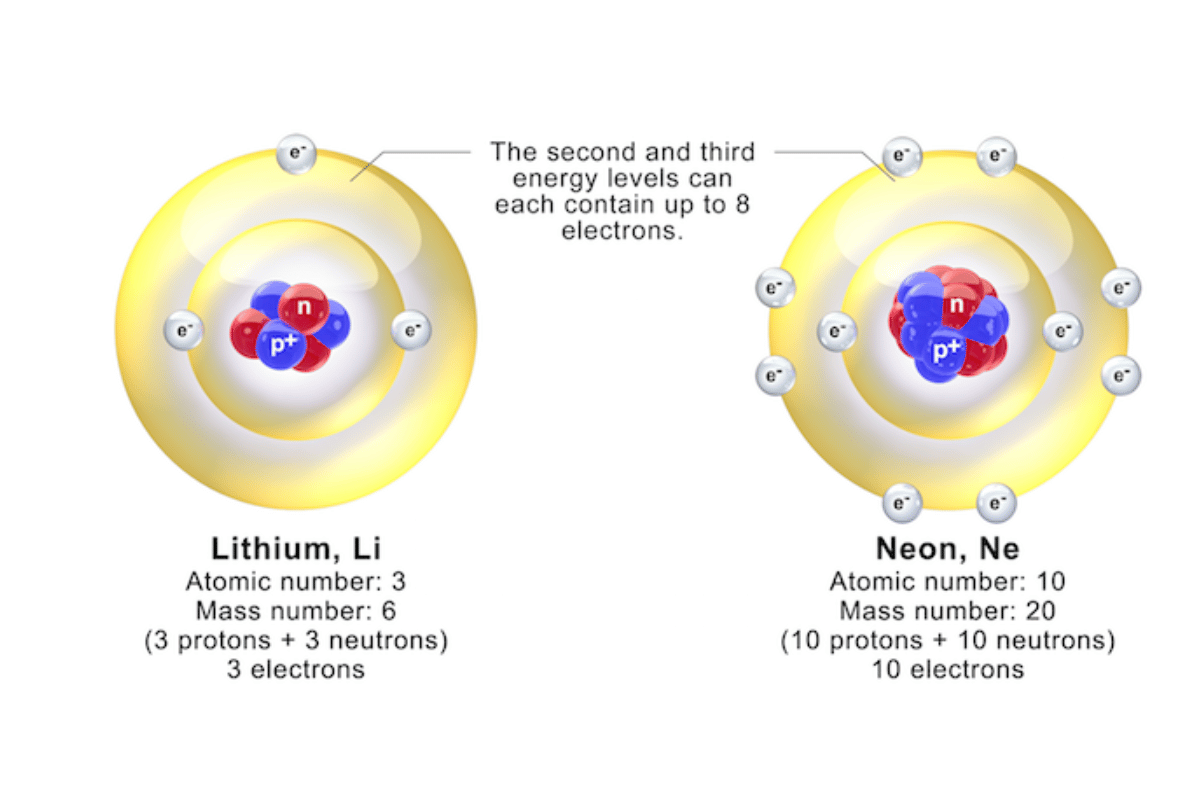
Chemical reactions and stability are highly influenced by neutral elements, those not bearing a charge. As noted in prominent educational resources, noble gases such as helium and neon, which are examples of neutrals, are inherently stable due to the fact that they have completely filled valence electron shells, making it difficult for them to form bonds with any other elements. This is why unreactive gases can always be found in many places, including light bulbs and inert atmospheres, when one carries out some chemical processes. On the other hand, the overall charge balance of these compounds shows how neutral atoms influence molecule’s properties and behavior during reactions. Therefore, understanding neutrality is crucial in theoretical chemistry and applied chemistry because it drives towards compound exploration and material discovery.

Understanding Charge in Neutral Atoms

I realize that when I think about a charge on neutral atoms, I must remember that a neutral atom has an equal number of electrons and protons, thus no overall charge. For example, there are six protons and six electrons present in carbon, which are neutral atoms. Furthermore, online platforms like Khan Academy or Chemguide stress that this balance guarantees stability while determining how atoms interact during reactions.

Technically speaking, the atomic number indicates the number of protons, which also represents the number of electrons for a neutral atom. Consider:

• Carbon (C):
• Atomic Number: 6
• Electrons: 6
• Protons: 6

With this basic understanding of charge, I am able to comprehend the conditions under which atoms remain uncharged, as well as their involvement in chemical bonding and reaction behavior affected by such neutrality. From reputable sources, including top educational websites, it becomes clear that changes within an atom’s number of protons identify its identity through atomic number, thereby setting up the basis for its subsequent chemistry.

Role of Electrons and Protons in Neutral Atoms

In analyzing the operations of electrons and protons in neutral atoms, it is apparent that both are vital to an atom’s structure and stability. Protons are located within the nucleus and carry a positive charge while electrons move around this nucleus with their negative charge. I have always believed that such balance is important; this information has driven me to some of the best educational sites among them, where, according to my research, protons number determines elements through atomic numbers, hence eliciting chemical behavior.

To be specific, consider these technical parameters:

• Hydrogen (H):
• Atomic Number: 1
• Electrons: 1
• Protons: 1
• Oxygen (O):
• Atomic Number: 8
• Electrons: 8
• Protons: 8
• Sodium (Na):
• Atomic Number: 11
• Electrons: 11
• Protons: 11

If I consider these elements, I find out that even minor changes in electron count can make an atom stray from being neutral and transform into ions with dissimilar chemistry reactions. Therefore, the interaction between protons and electrons determines their form and reactiveness, thus supporting compound formation. This understanding allows me to appreciate the complexity of chemical reactions, as indicated across many academic resources.

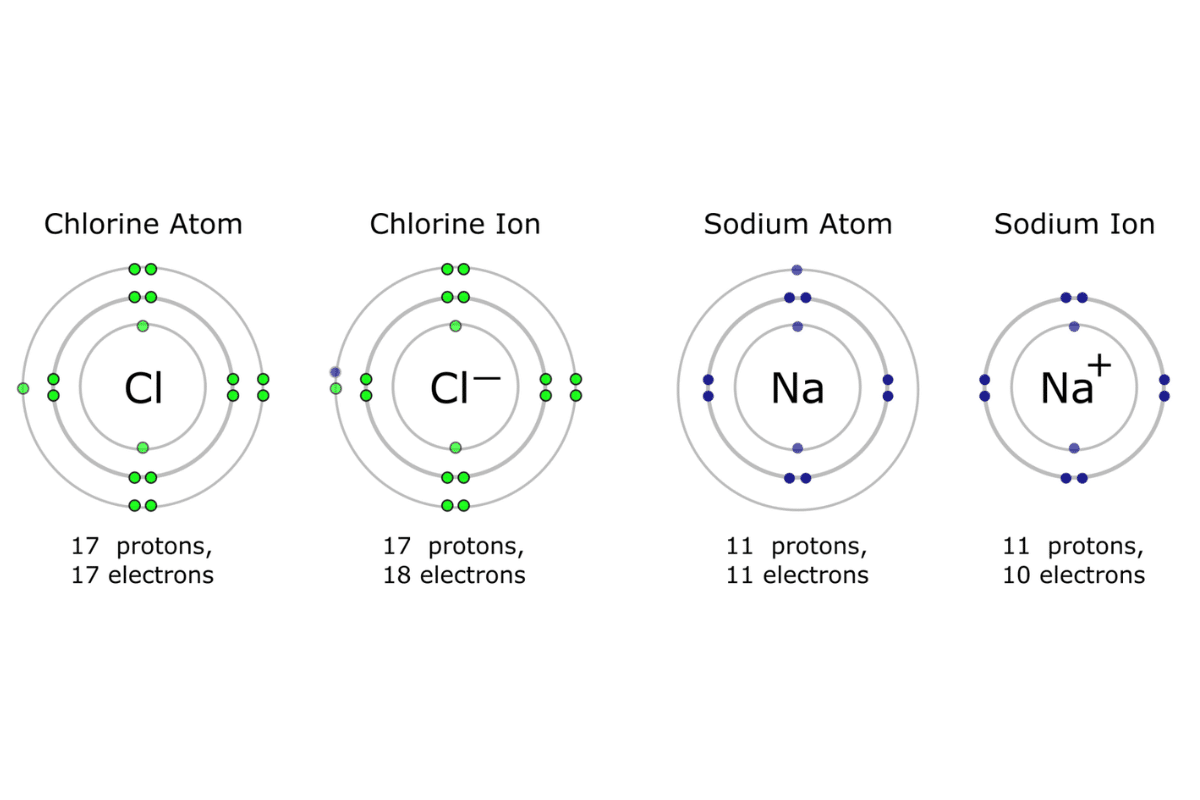
Comparison between Ions and Neutral Atoms

In my investigation of the differences between ions and neutral atoms, I found that they are primarily about the balance of protons and electrons. Neutral atoms have equal protons and electrons and, hence, have no charge. However, when an atom gains or loses electrons, they become ions. This shift in the amount of electrons changes its electric charge and chemical properties.

For example, a sodium atom (Na) turns into a sodium ion (Na⁺) after being stripped off one electron. The following listed technical aspects demonstrate this scenario:

• Sodium Atom (Na):
• Atomic Number: 11
• Electrons: 11
• Protons: 11
• Charge: 0 (neutral)
• Sodium Ion (Na⁺):
• Atomic Number: 11
• Electrons: 10 (one lost)
• Protons: 11
• Charge: +1 (positive ion)
• Similarly, chlorine gains another electron to become chloride ion Cl⁻.
• Chlorine Atom (Cl):
• Atomic Number: 17
• Electrons: 17
• Protons: 17
• Charge: 0 (neutral)
• Chloride Ion(Cl⁻):
• Atomic number :17,
• Electrons :18(one gained),
• Protons :17,
• Charge :-1(negative ion).

Through some research using sources from reputable texts, I have learned how these changes can drastically alter how ions interact chemically compared to their neutral counterparts. This knowledge has helped me delve further into chemical bonding and the peculiarities of substances in different states.

Conclusion:

In conclusion, neutral elements are important in the field of chemistry since they are considered stable with balanced charges which act as a benchmark for understanding ions and their interactions. All matter comprises neutral atoms with similar numbers of electrons and protons. It should be noted that the transition from neutral atoms to ions changes the charge of an element and substantially influences its bondability and reactivity. By studying the properties of neutral elements, we obtain crucial information about how different substances behave during chemical reactions, which helps us understand more complicated chemical processes. This information is a basis for further studies in elemental behavior and chemical interaction within the broader scope of the scientific field.

Reference Sources

1. Chemistry LibreTexts: An extensive online resource providing detailed coverage of chemical principles, including the properties of neutral elements and their role in reactions and bonding. Visit Chemistry LibreTexts
   2. Khan Academy: Offers comprehensive educational materials on basic chemistry concepts, including neutral atoms and ions, with engaging explanations and interactive exercises. Visit Khan Academy
      3. Royal Society of Chemistry: A reputable professional organization that publishes articles and educational resources focused on the various branches of chemistry, including information on neutral elements and their significance in the field. Visit Royal Society of Chemistry

Frequently Asked Questions (FAQs)

Q1: What is a neutral element?

A neutral element is an atom that has an equal number of protons and electrons, resulting in no overall charge. This balance of positive and negative charges keeps the atom electrically neutral.

Q2: How do neutral elements differ from ions?

Neutral elements have no charge, while ions are atoms that have gained or lost electrons, resulting in a positive or negative charge. This charge affects their chemical properties and reactivity.

Q3: Why are neutral elements important in chemistry?

Neutral elements serve as the fundamental building blocks of matter. Understanding their properties aids in predicting how they will behave in chemical reactions, forming the basis for more complex studies in the field.

Q4: Can neutral elements form compounds?

Yes, neutral elements can form compounds through chemical bonding. When they react, they may either share electrons (covalent bonding) or transfer electrons (ionic bonding), resulting in diverse chemical compounds.

Q5: What happens to an element when it becomes ionized?

When an element becomes ionized, it either loses electrons, becoming a positively charged cation, or gains electrons, resulting in a negatively charged anion. This transformation alters the element’s reactivity and bonding properties.